In einem einfachen Modell könnte für einen Wettbewerber die Kontrolle der Stückkosten mehr sein als nur die Abschwächung von bspw. Marktschwankungen in den Inputkosten.
Eine solche Kontrolle bspw. der Inputkosten, z. B. über eigene Lieferketten oder Prozesse, Hedging von Materialkosten, oder andere Maßnahmen in die Stückkosten könnte u. U. zu Verschiebungen in Gleichgewichten zwischen Wettbewerbern führen und damit (möglicherweise) zu einer Umverteilung der Gewinne zwischen den Wettbewerbern.
Ein ganz einfaches Modell des Oligopolwettbewerbs
Es gibt einige bekannte Modelle für den Oligopolwettbewerb.
Bei dem hier im Folgenden verwendeten Modell handelt es sich um ein Modell des Mengenwettbewerbs (Cournot-Modell), bei dem die Wettbewerber entscheiden können, wie viel sie produzieren, um den Gewinn zum resultierenden Marktpreis zu maximieren. Diese Art von Modell wird typischerweise in Situationen betrachtet, in denen die Wettbewerber ein identisches Produkt herstellen.
Wir gehen von einer einfachen, linearen Beziehung zwischen Preis und Angebots- bzw. Nachfragemenge aus (Abbildung 1).
Abbildung 1: Lineare Beziehung zwischen Preis und Menge—je höher der Preis, desto niedriger die Nachfrage

Gewinne und Mengen in einem Monopolmodell
Um sich mit dieser Art von Modell vertraut zu machen, zunächst ein Blick auf eine Monopolsituation.
Der Gewinn (Profit) des Monopolisten ist hier eine Funktion der Produktmenge, des Preises und den Kosten für die Produktion dieser Menge. Alles in allem ist der Profit
– Preis multipliziert mit der Menge; minus
– Variable Kosten (hier nur Stückkosten); minus
– (Fixkosten; hier in diesem einfachen Modell auf 0 gesetzt.)
Die Abhängigkeit zwischen Preis und Menge führt hier zu einer Nichtlinearität, so dass der Gewinn in Abhängigkeit von der Menge wie folgt aussieht (bei festen Stückkosten von 1, Abbildung 2):
Abbildung 2: Der Gewinn als Funktion der Menge hat ein klares Maximum
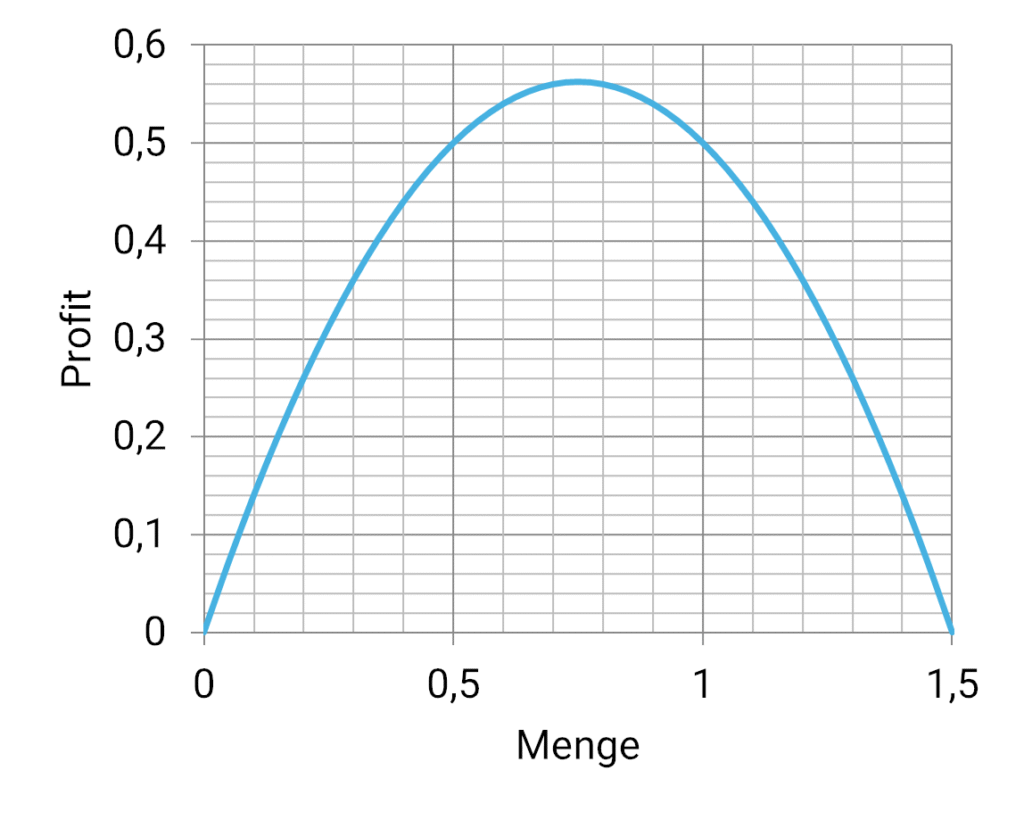
Das bedeutet, dass es eine Menge gibt, die den Gewinn maximiert, wenn die Preis-Nachfragemengen-Relation und die Stückkosten gegeben sind. Das nachstehende Diagramm zeigt die optimale Menge und den maximalen Gewinn, der bei der Produktion der optimalen Menge in Abhängigkeit von den Stückkosten erzielt würde (auch hier gibt es eine nicht lineare Beziehung zwischen Stückkosten und maximalem Gewinn, Abbildung 3).
Abbildung 3: Der maximale Gewinn steigt mit niedrigeren Stückkosten
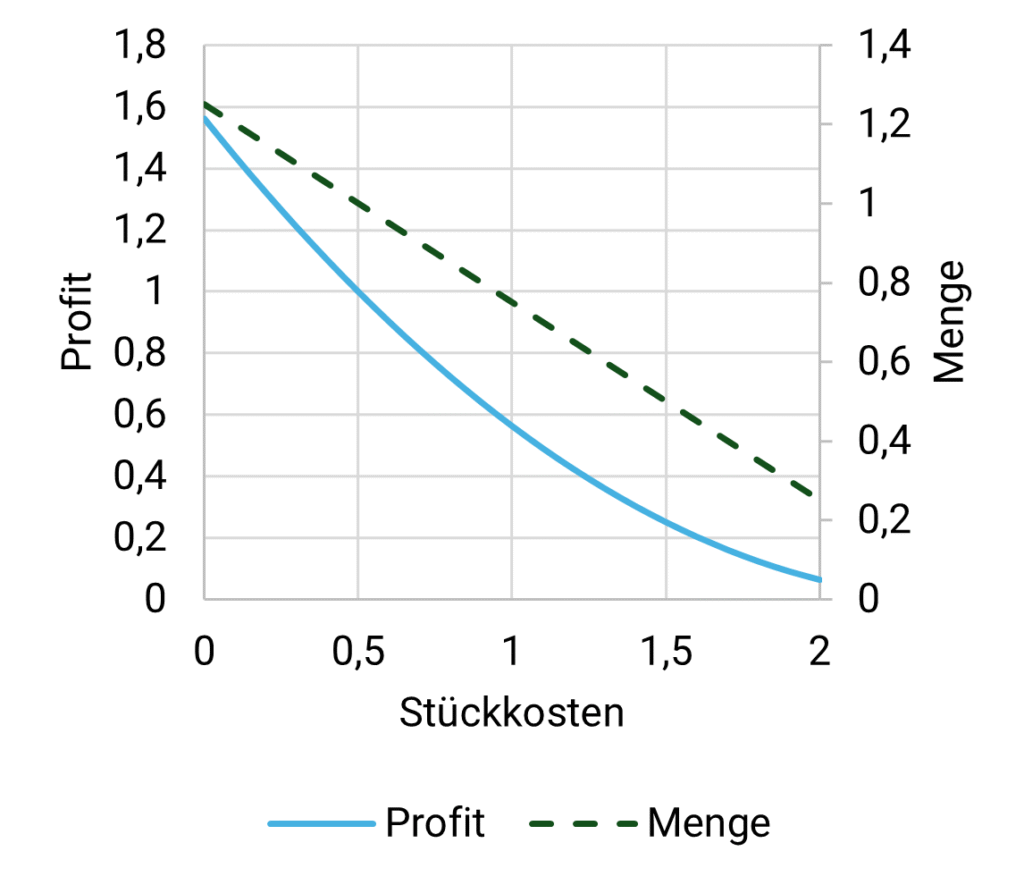
Wenn bspw. die Inputkosten in die Stückkosten eine kontrollierbare Komponente haben, könnte eine solche Kontrolle potenziell dazu genutzt werden, höhere Gewinne zu erzielen, indem die Stückkosten niedriger gehalten werden könnten, wenn z. B. die Inputkosten steigen.
In einem Monopolumfeld ist die Situation recht einfach, da in diesem Modell die angebotene Menge vollständig unter der Kontrolle des Produzenten steht und die Preis-Nachfrage Relation bekannt ist; sobald Wettbewerb herrscht, werden die Dinge dynamischer.
Einführung von Wettbewerb – niedrigere Gewinne im Modell in einem Duopol
Bei dem Übergang vom Monopol zu einem Duopol wird der Monopolgewinn nicht einfach auf zwei Wettbewerber umverteilt: Der maximale Gesamtgewinn, der bei zwei gleichartigen Wettbewerbern erzielt werden kann, ist niedriger als der im Monopol bei gleichzeitig höherer Menge (vorausgesetzt, es wird kein Kartell gebildet; Abbildung 4, die Stückkosten betragen wieder 1).
Abbildung 4: Die maximalen Gewinne eines Duopols im Nash-Gleichgewicht sind, bei gleichzeitig steigender Menge, niedriger als die im Monopols

Wettbewerb senkt den Gesamtgewinn im System, wenn jeder Wettbewerber seinen Output so wählt, dass er optimal ist, wenn die Erwartungen des Wettbewerbers über das Verhalten des anderen Wettbewerbers erfüllt sind (Nash-Gleichgewicht).
Dämpfung eines Stückkostenanstiegs könnte (im Modell) Vorteile bringen
In dem einfachen Modell hier werden die Stückkosten für einen der Wettbewerber konstant gehalten (gleich 1, unabhängig von der Menge). Unter diesen Bedingungen ist es einfach, die maximalen Gewinne der Wettbewerber (Kontrolleur) bei Änderungen des Stückpreises für den anderen Wettbewerber (Preisnehmer) abzuleiten (Abbildung 5).
Abbildung 5: Ein Kostenkontrolleur könnte bei höheren Input-/Stückkosten einen monopolähnlichen Vorteil haben
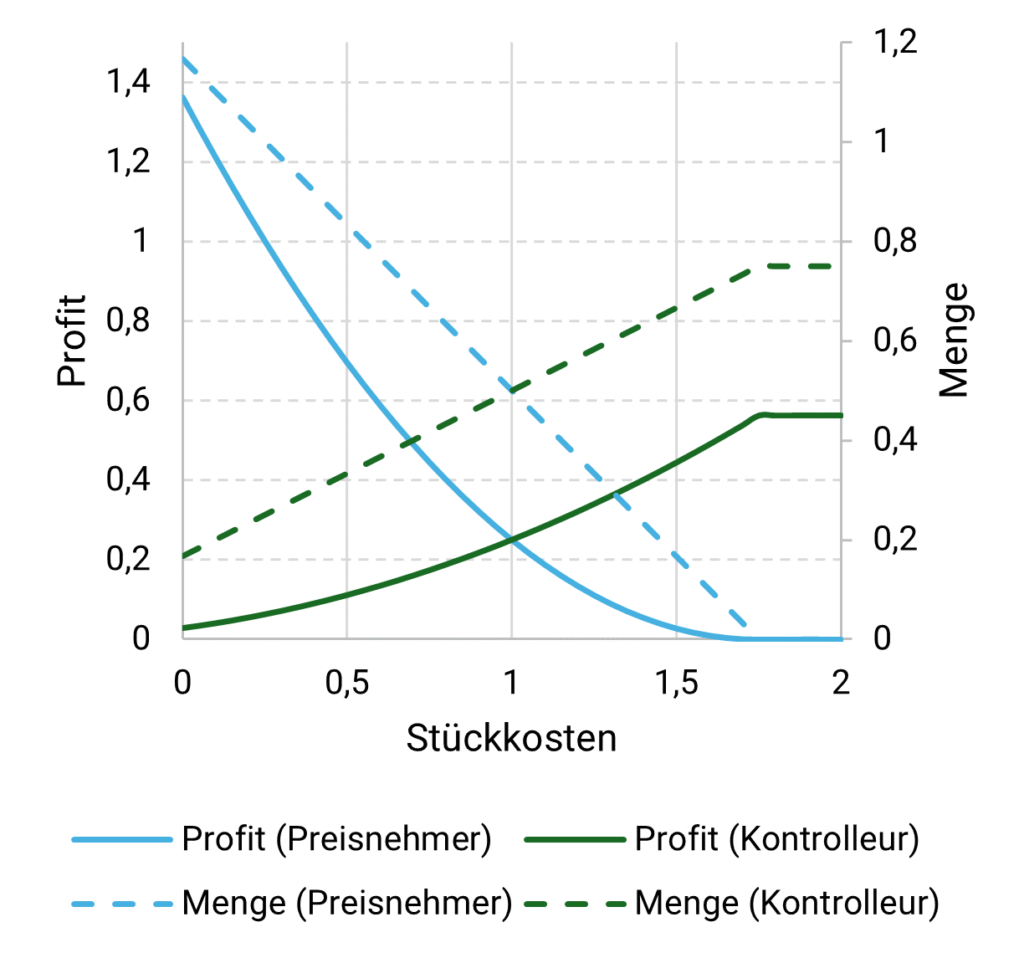
Durch die Kostenkontrolle ändert sich das Bild im Vergleich zum einfachen Duopol etwas: Bei Stückkosten, die höher sind als die kontrollierten Kosten, steigt der Profit des Wettbewerbers, der die Stückkosten kontrolliert, bis dieser das Monopolniveau erreicht (unter den fixen Stückkosten). Bei Stückkosten, die unter den kontrollierten liegen, verzeichnet der andere Wettbewerber jedoch rasch steigenden Profit, während der Profit des kontrollierenden Wettbewerbers sinkt. Eine wichtige Beobachtung in diesem Zusammenhang ist, dass die Gewinnreaktion auf die (Input-)Stückkosten nicht einfach symmetrisch ist.
Bei den obigen Ausführungen wurden, neben dem an sich schon einfachen Modell, einige vereinfachende Annahmen zugrunde gelegt, z. B. eine Kostenkontrolle unabhängig von der Menge.
Einige abschließende Bemerkungen
Das obige Beispiel gibt einen kleinen Einblick in die möglichen Dynamiken von (Input-)Kostenkontrollen in bestimmten (Modell-)Wettbewerbssituationen.
Ein möglicher nächster Schritt könnte die Betrachtung von Interaktionen/Reaktionen zwischen Wettbewerbern unter Verwendung von Kostenkontrollen sein, was zusätzliche Dynamik und spieltheoretische Überlegungen hervorrufen könnte.
Hinweis: Die Simulationen und Ausführungen wurden mit großer Sorgfalt erstellt, aber Fehler und Ungenauigkeiten sind nicht auszuschließen. Weiterhin kann das Modell für keine Anwendung passend oder sinnvoll sein.